相关性
Pearson积矩相关
皮尔逊相关系数(Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs, 用r表示)。皮尔逊相关系数适用场景是呈正态分布的连续变量,当数据集的数量超过500时,可以近似认为数据呈正态分布,因为按照中心极限定理,当数据量足够大时,可以认为数据是近似正态分布的。
使用条件:
- 两个变量是连续数据;
- 符合正态分布,所以样本容量尽量要超过30个;
- 两个变量的观测值是成对的,每对观测值之间相互独立。
- 两变量为线性关系。
皮尔逊相关系数公式:
样本皮尔逊相关系数公式:
协方差其实已经是在计算X与Y的相关程度了。但是如果X与Y的数据分布的很离散,其协方差就很大,而实际上x、y的相关程度较小,所以用协方差值来度量相关程度是不合理的。而且协方差是有量纲的量。举个例子,X表示身高,单位是cm,Y表示体重,单位是kg,那协方差计算出来后单位是cm·kg。假设我们想比较身高和体重的相关度与身高和年龄的相关度,会发现,两者的单位不一致,不太好比较。所以,为了消除量纲的影响,对协方差除以相同的量纲的量,就得到了相关系数。也可看成两个n维向量的夹角余弦。
在解释Pearson相关系数时,注意:
仅根据Pearson相关即得出两个变量的一般关系是不合理的,它只是表述两个变量线性关系的程度。只有进行过适当控制的试验才能确定是否存在因果关系。
Pearson 相关系数对极值数据非常敏感。离群值会极大地改变该系数值。可用散点图或拟合曲线确定离群值,考虑删除与异常的一次性事件(特殊原因)相关的数据值。
同时应该调查异常值,因为他们能够提供关于数据或过程的有用信息。
低 Pearson 相关系数并不意味着变量之间不存在任何关系。变量之间可能具有非线性关系。要以图形方式检查是否存在非线性关系。
Spearman秩次相关
Spearman相关系数又称秩相关系数,是利用两变量的秩次大小作线性相关分析,对原始变量的分布不作要求,属于非参数统计方法,适用范围要广些。
斯皮尔曼相关系数不受离群值影响,适用于非线性。对于斯皮尔曼相关系数,我们不需要关心数据如何变化,符合什么样的分布,只需要关心每个变量对应数值的位置。如果两个变量的对应值,在各组内的排列顺位是相同或类似的(或者理解为一个变量是另外一个变量的严格单调函数),则具有显著的相关性。
注意:
- 若非等距的连续变量,因为分布不明,可用Pearson相关/也可用Spearman相关,对于完全等级离散变量必用Spearman相关。
- 当资料不服从双变量正态分布或总体分布未知或原始数据是用等级表示时,宜用Spearman 相关。
- 若不恰当用了等级相关,可能得相关系数偏小或偏大结论而考察不到不同变量间存在的密切关系。
- 对一般情况默认数据服从正态分布的,故用Pearson分析方法。
- 基于秩的估计量适用于小规模的数据集以及特定的假设检验。
简单来说,皮尔逊要求两个连续变量是线性的,斯皮尔曼要求两个连续或顺序变量是单调的。
对 Pearson 和 Spearman 系数进行比较
 Pearson = +0.851,Spearman = +1
Pearson = +0.851,Spearman = +1
 Pearson = -0.799,Spearman = -1
Pearson = -0.799,Spearman = -1
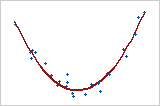 图形显示非常强的关系,但Pearson 系数和 Spearman 系数都近似 0。
图形显示非常强的关系,但Pearson 系数和 Spearman 系数都近似 0。
相关系数对应的相关强度如下:
- 0.8-1.0 极强相关
- 0.6-0.8 强相关
- 0.4-0.6 中等程度相关
- 0.2-0.4 弱相关
- 0.0-0.2 极弱相关或无相关